Occupational exposure limits (OELs, TLVs, PELs, etc.) can be expressed in parts per million (ppm) only if the substance exists as a gas or vapour at normal room temperature and pressure. This is why exposure limits are usually expressed in mg/m3. However, some OELs may be expressed in units such as fibres/cc (e.g., for asbestos). OELs for metals, salts and other compounds that do not form vapours at room temperature and pressure are expressed in mg/m3 only.

The ACGIH booklet "Threshold Limit Values (TLVs™) for Chemical Substances and Physical Agents and Biological Exposure Indices (BEIs™)" uses the formulas:

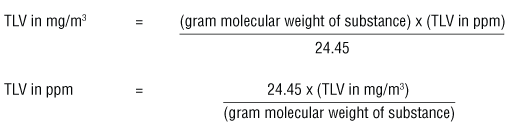
These formulas can be used when measurements are taken at 25°C and the air pressure is 760 torr (= 1 atmosphere or 760 mm Hg).

Gram molecular weight is the molecular weight (MW) of a substance expressed in grams. For example, the gram molecular weight for toluene is 92.13 g. since the molecular weight is 92.13. A gram molecular weight is also called a gram mole.

The number 24.45 in the equations above is the volume (liters) of a mole (gram molecular weight) of a gas or vapour when the pressure is at 1 atmosphere (760 torr or 760 mm Hg) and at 25°C.

To convert mg/m3 to ppm at other temperatures and pressures, one must calculate the volume of 1 gram molecular weight of an airborne contaminant (e.g. 92.13 grams of toluene) by using the formula:

V = (RT/ P)

where R is the ideal gas constant; T is the temperature in  kelvins (273.16 + T°C); and P is the pressure in mm Hg. This information can be substituted in the formulas for converting between mg/m3 and ppm.

where the value of R is 62.4 L torr/mol K when the temperature (T) is in kelvins (K), (K =273.16 + T°C), the pressure is expressed in units of mm Hg (1 mmHg = 1 torr), and the volume is in liters. The gas constant can have different values if the temperature and pressure are expressed in different units from those in the above equation.